Ôn thi vào lớp 10: Bốn cách chứng minh tứ giác trong Toán hình đơn giản, dễ nhớ
Chứng minh “Tứ giác nội tiếp” là dạng bài tập thông dụng , thường xuyên gặp ở các bài thi Toán vào lớp 10 THPT, thí sinh cần đặc biệt lưu ý.
Để giúp học sinh nắm chắc kiến thức và kỹ năng, thầy Nguyễn Quyết Thắng – giáo viên môn Toán tại Hệ thống Giáo dục HOCMAI hướng dẫn học sinh một số phương pháp chứng minh tứ giác nội tiếp đơn giản, hiệu quả hơn, từ đó có thể dành trọn điểm ở phần này.
Chứng minh tứ giác nội tiếp là ta cần chứng minh 4 đỉnh của tứ giác nằm trên cùng một đường tròn. Dạng bài tập này sẽ có nhiều mức độ để thử thách các em học sinh từ trung bình đến giỏi.
Thầy Thắng chỉ ra 4 phương pháp chứng minh tứ giác nội tiếp đơn giản, dễ nhớ:
Thầy Nguyễn Quyết Thắng – giáo viên môn Toán tại Hệ thống Giáo dục HOCMAI.
Phương pháp 1 , chứng minh tứ giác có tổng hai góc đối bằng 180 độ. Phương pháp này được xuất phát từ chính định nghĩa của tứ giác nội tiếp (Một tứ giác có bốn đỉnh cùng nằm trên một đường tròn gọi là tứ giác nội tiếp đường tròn).
Nội dung của phương pháp này như sau: “Nếu tứ giác ABCD có tổng hai góc đối bằng 180 độ thì tứ giác đó nội tiếp”. Hệ quả của nội dung này là: Nếu góc BAD = góc BCD = 90 độ thì tứ giác ABCD nội tiếp đường tròn tâm O đường kính BD. Nếu tổng hai góc kề bù EAD = BCD thì tứ giác ABCD nội tiếp
Phương pháp 2 , chứng minh tứ giác có góc ngoài tại một đỉnh bằng góc trong của đỉnh đối diện. Ở phương pháp này, học sinh chú ý phải nhìn đúng hình đúng góc, nếu không sẽ bị tình trạng chứng minh sai nhưng kết quả đúng và ảnh hưởng tới những câu tiếp theo.
Video đang HOT
Cụ thể, khi đề bài cho tứ giác ABCD và chứng minh được góc ngoài tại đỉnh A bằng góc C của tứ giác (góc A và góc C đối đỉnh) thì có thể kết luận tứ giác ABCD là tứ giác nội tiếp.
Phương pháp 3, chứng minh hai đỉnh cùng kề một cạnh, cùng nhìn cạnh đó dưới hai góc bằng nhau và bằng 90 độ. Phương pháp này áp dụng khi đề bài cho tứ giác ABCD và những dữ kiện gợi ý tính được rằng DAC = DBC = 90 độ. Từ đó, học sinh có thể kết luận tứ giác ABCD nội tiếp đường tròn.
Phương pháp 4 , chứng minh bốn đỉnh của một tứ giác cách đều một điểm xác định. Nếu đề bài cho trước một đường tròn tâm O có bán kính R thì bất kỳ điểm nào nằm trên đường tròn đều cách tâm một khoảng đúng bằng bán kính.
Theo thầy Thắng hướng dẫn, dựa vào tính chất này, học sinh có thể dễ dàng chứng minh một tứ giác nội tiếp một đường tròn.
Ví dụ: Cho một điểm O cố định và tứ giác ABCD. Nếu học sinh chứng minh được bốn điểm A, B, C, D cách đều điểm O với khoảng cách bằng R, tức OA = OB = OC = OD = R thì điểm O chính là tâm đường tròn đi qua bốn điểm A, B, C, D. Hay nói cách khác, tứ giác ABCD nội tiếp đường tròn tâm O bán kính R.
Ngoài ra, thầy cũng đưa ra một số lưu ý khi làm bài chứng minh tứ giác nội tiếp. Nếu nhận thấy khả năng tứ giác đó rơi vào một trong các trường hợp đặc biệt (hình chữ nhật, hình vuông, hình thang cân), ta có thể chứng minh tứ giác đó là hình đặc biệt và kết luận tứ giác nội tiếp đường tròn. Vì hình chữ nhật, hình vuông, hình thang cân đều nội tiếp đường tròn.
Bên cạnh đó, trong quá trình làm bài, học sinh nên vẽ hình rõ ràng, dễ nhìn và tránh vẽ hình tại một số trường hợp đặc biệt. Các kí hiệu góc, đoạn thẳng bằng nhau cần được đánh dấu rõ ràng.
Trong quá trình làm bài thi, học sinh nên bám vào giả thiết, kiến thức đã học để làm bài cho hiệu quả. Những yêu cầu của đề bài cũng có thể là hướng gợi ý để giải quyết bài toán. Và đặc biệt, không dùng những điều đang cần chứng minh để chứng minh lại chúng.
Làm văn thế nào để đạt điểm cao trong kỳ thi tuyển sinh lớp 10?
Trong đề thi tuyển sinh lớp 10, chương trình tập làm văn lớp 9 chiếm điểm số khá cao. Muốn làm tốt phần này, thí sinh cần nắm được phương pháp và kĩ năng làm các dạng bài nghị luận.
Theo lịch đã công bố, tháng 6 là thời điểm nhiều địa phương trên cả nước sẽ tổ chức kỳ thi tuyển sinh vào lớp 10, trong đó Ngữ văn là bài thi bắt buộc. Trao đổi với VOV.VN về phương pháp làm bài thi môn Ngữ văn, cô Đỗ Khánh Phượng, giáo viên bộ môn Ngữ văn tại Hệ thống Giáo dục HOCMAI cho rằng, nghị luận là đơn vị kiến thức trọng tâm trong chương trình tập làm văn lớp 9. Có 2 dạng nghị luận mà học sinh cần lưu ý là nghị luận xã hội và nghị luận văn học. Phần này thường chiếm từ 6 đến 8 điểm tùy địa phương.
Cô Đỗ Khánh Phượng đưa ra một số lời khuyên cho thí sinh khi làm bài thi môn Ngữ văn khi thi vào lớp 10.
Lưu ý khi làm dạng bài nghị luận xã hội
Cô Phượng cho biết, các dạng bài nghị luận xã hội nhìn chung đều vận dụng linh hoạt các thao tác lập luận giải thích, phân tích, chứng minh, bác bỏ, bình luận. Trong đó, ba thao tác giải thích, chứng minh và bình luận là thường được sử dụng nhất.
"Tùy mỗi địa phương, yêu cầu về hình thức phần nghị luận xã hội sẽ khác nhau. Phần lớn sẽ là viết đoạn văn hoặc bài văn ngắn (độ dài một trang giấy thi). Để làm đoạn văn nghị luận xã hội, học sinh cần bám sát yêu cầu đề để xác định trọng tâm đoạn văn", cô Phượng chia sẻ.
Ví dụ, đề nghị luận xã hội vào 10 năm 2020 tại Thanh Hóa là: "Từ nội dung đoạn trích phần Đọc - hiểu, em hãy viết một đoạn văn (khoảng 200 chữ) trình bày về sự cần thiết của việc vươn lên từng ngày ở mỗi người". Với đề bài này, học sinh cần xác định được trọng tâm của đề là sự cần thiết của việc vươn lên từng ngày ở mỗi người.
Trong chương trình tập làm văn lớp 9, dạng bài văn nghị luận xã hội được chia làm ba loại nhỏ, nghị luận về một vấn đề tư tưởng đạo lí, nghị luận về một sự việc, hiện tượng đời sống và nghị luận về một vấn đề xã hội trong tác phẩm văn học. Khi đọc đề, thí sinh cần xác định được loại bài nghị luận xã hội vì mỗi loại sẽ có một cách làm khác nhau.
Cụ thể, đề nghị luận về một tư tưởng đạo lí sẽ thiên về những vấn đề mang tính lí thuyết, như tình mẫu tử, tình đồng bào, tính trung thực, lòng dũng cảm, mục đích sống... nên các thao tác giải thích, phân tích, bình luận sẽ sử dụng nhiều.
Đề nghị luận về một sự việc, hiện tượng đời sống lại hướng vào những vấn đề thực tiễn như bạo lực gia đình, vi phạm luật giao thông, các hoạt động từ thiện, bệnh thành tích... Chính vì vậy, dạng bài này đề cao dẫn chứng. Do đó, học sinh cần lấy dẫn chứng tiêu biểu, phổ biến và biết cách phân tích dẫn chứng để đưa vào bài. Tránh tình trạng lấy dẫn chứng tràn lan, sa đà vào kể chuyện hoặc lấy dẫn chứng theo kiểu liệt kê mà không phân tích dẫn chứng.
"Dạng nghị luận về một vấn đề xã hội trong tác phẩm văn học thường được đưa vào các đề thi, tuy nhiên các em cần lưu ý, đó vẫn là đề nghị luận xã hội, không phải đề nghị luận văn học, nên không được sa đà vào phân tích tác phẩm. Đối với dạng đề này, học sinh phải biết mở đoạn bằng cách dẫn dắt vấn đề từ nhân vật trong tác phẩm/đoạn trích (ngữ liệu)", cô Phượng nhấn mạnh.
Phương pháp làm dạng bài nghị luận văn học
Với phần nghị luận văn học, cô Đỗ Khánh Phượng cho rằng đây là dạng bài có số điểm cao nhất trong các đề thi vào 10. Tùy đề thi tại mỗi địa phương mà học sinh sẽ viết bài văn hoặc đoạn văn.
Dù là đoạn văn hay bài văn, học sinh cũng cần xác định đúng vấn đề cần nghị luận. Đây là khâu quan trọng trong quá trình làm bài, nếu các em không xác định được vấn đề nghị luận, bài viết sẽ lan man, không có trọng tâm, thiếu ý hoặc lạc đề.
"Muốn làm tốt phần này, các em nên triển khai vấn đề nghị luận thành các luận điểm, vận dụng tốt các thao tác lập luận, kết hợp chặt chẽ giữa lí lẽ và dẫn chứng", cô Phượng nêu rõ.
Với nghị luận về truyện, các đề thường thiên về cảm nhận nhân vật văn học. Các đề nghị luận về thơ thường thiên về cảm nhận một đoạn thơ. Yêu cầu cơ bản để làm được nghị luận văn học là phải nắm được hoàn cảnh sáng tác, chủ đề, nội dung chi tiết và các đặc điểm nghệ thuật cụ thể của mỗi tác phẩm.
Bên cạnh đó, để đạt điểm cao, cô Phượng lưu ý học sinh phải biết sử dụng thao tác lập luận so sánh với những văn bản có cùng chủ đề để có thể mở rộng, đào sâu vấn đề cần nghị luận, có như thế bài làm mới ấn tượng./.
Cách làm bài 'đại từ quan hệ' trong đề thi Tiếng Anh vào lớp 10  Đại từ quan hệ là kiến thức khá khó và thường xuyên xuất hiện trong đề thi tiếng Anh vào lớp 10 của nhiều tỉnh thành trên cả nước. Ảnh minh họa. Dưới đây là những lưu ý của thầy Nguyễn Trung Nguyên, giáo viên tiếng Anh tại Hệ thống Giáo dục HOCMAI nhằm giúp các em ôn tập tốt phần kiến thức...
Đại từ quan hệ là kiến thức khá khó và thường xuyên xuất hiện trong đề thi tiếng Anh vào lớp 10 của nhiều tỉnh thành trên cả nước. Ảnh minh họa. Dưới đây là những lưu ý của thầy Nguyễn Trung Nguyên, giáo viên tiếng Anh tại Hệ thống Giáo dục HOCMAI nhằm giúp các em ôn tập tốt phần kiến thức...
 Vợ Giao Heo gục ngã khi biết tin chồng mất, tiết lộ lời hứa dang dở gây xót xa02:33
Vợ Giao Heo gục ngã khi biết tin chồng mất, tiết lộ lời hứa dang dở gây xót xa02:33 Danh tính Thạc sĩ Việt mập mờ với ai xong cũng gửi cho người ta "feedback" dài như tờ sớ00:16
Danh tính Thạc sĩ Việt mập mờ với ai xong cũng gửi cho người ta "feedback" dài như tờ sớ00:16 Tun Phạm 'công khai' có em bé, lộ danh tính vợ chưa cưới gây 'sốc' CĐM?02:54
Tun Phạm 'công khai' có em bé, lộ danh tính vợ chưa cưới gây 'sốc' CĐM?02:54 Võ sĩ Kota Miura công khai bạn gái hơn 14 tuổi, lộ nhiều khoảnh khắc "ngọt ngào"02:49
Võ sĩ Kota Miura công khai bạn gái hơn 14 tuổi, lộ nhiều khoảnh khắc "ngọt ngào"02:49 Tổng tài nghi ra lệnh "tác động" nhân viên quán cà phê kêu oan, chỉ tự vệ02:34
Tổng tài nghi ra lệnh "tác động" nhân viên quán cà phê kêu oan, chỉ tự vệ02:34 Chồng cũ Xoài Non giảm 20kg hậu mất vợ, 1 sao nữ gãy chân lộ diện tương tác sốc?02:43
Chồng cũ Xoài Non giảm 20kg hậu mất vợ, 1 sao nữ gãy chân lộ diện tương tác sốc?02:43 TikToker Giao Heo qua đời vì tai nạn giao thông, xót xa bài đăng cuối cùng02:43
TikToker Giao Heo qua đời vì tai nạn giao thông, xót xa bài đăng cuối cùng02:43 Ấm lòng bà cháu ở Lạng Sơn mở cửa cho hơn 30 bộ đội nghỉ nhờ00:45
Ấm lòng bà cháu ở Lạng Sơn mở cửa cho hơn 30 bộ đội nghỉ nhờ00:45 Vợ Giao Heo luôn "dạ - thưa", được chồng cưng chiều, 5 năm mất 3 người thân02:52
Vợ Giao Heo luôn "dạ - thưa", được chồng cưng chiều, 5 năm mất 3 người thân02:52 Con trai Hòa Minzy nói câu "xót lòng" khi ít gặp mẹ, phản ứng dân mạng tan chảy02:44
Con trai Hòa Minzy nói câu "xót lòng" khi ít gặp mẹ, phản ứng dân mạng tan chảy02:44 Ông Đỗ Văn Hữu 'van xin' chủ đất, toàn bộ tài sản 'tích góp' đã dồn vào căn nhà02:49
Ông Đỗ Văn Hữu 'van xin' chủ đất, toàn bộ tài sản 'tích góp' đã dồn vào căn nhà02:49Tin đang nóng
Tin mới nhất

Còn nhiều băn khoăn về chứng nhận giỏi cấp tỉnh với học sinh điểm IELTS cao

Việc thực hiện chương trình, SGK mới còn nhiều khó khăn

Cấp phép tổ chức thi chứng chỉ HSK trở lại

Banner tìm hiểu ngày 22/12 của Trường ĐH Tôn Đức Thắng in hình lính Mỹ

Nhiều tỉnh cho học sinh nghỉ Tết hơn 10 ngày, Hà Nội lý giải nghỉ 8 ngày

Trường ĐH Kiên Giang dự kiến tuyển hơn 1.600 chỉ tiêu năm 2023

Trường Đại học Hồng Đức nâng cao chất lượng đào tạo sinh viên ngành giáo dục mầm non

Học sinh Hà Giang nghỉ Tết Quý Mão 12 ngày, từ 27 tháng Chạp

Nhiều tiết dạy sáng tạo tại hội thi giáo viên dạy giỏi Hà Nội

Trường Đại học Kinh tế Quốc dân công bố Đề án tuyển sinh đại học năm 2023

Tuyển sinh 2023: Đại học Kinh tế Quốc dân công bố đề án tuyển sinh

Cần cẩn trọng lựa chọn nhân sự, ra đề thi
Có thể bạn quan tâm

'Tử chiến trên không' vượt mốc 100 tỉ sau một tuần ra rạp
Hậu trường phim
23:49:53 24/09/2025
Nga tung chiến thuật "độn thổ" vây bọc Ukraine ở pháo đài chiến lược
Thế giới
23:48:15 24/09/2025
Ăn bát bún cá dính xương, người đàn ông thủng ruột non
Sức khỏe
23:44:59 24/09/2025
Đình Tú Ngọc Huyền khoe ảnh cưới lãng mạn giữa lòng Hà Nội
Sao việt
23:43:44 24/09/2025
19 bài hát không bao giờ được ra mắt của Mỹ Tâm tiết lộ quan hệ bí ẩn với ân nhân làm nên sự nghiệp
Nhạc việt
23:30:34 24/09/2025
Nam thanh niên bị khởi tố vì mua bán 5 cá thể rùa Trung Bộ nguy cấp
Pháp luật
23:30:30 24/09/2025
Nữ sinh vào nhà nghỉ, nhắn tin nhờ mẹ chuyển 300 triệu đồng rồi "biến mất"
Tin nổi bật
23:28:19 24/09/2025
Vợ lén mua đồng hồ 3 triệu đồng, tôi ngã ngửa khi biết đó là quà tặng ai
Góc tâm tình
23:21:14 24/09/2025
Các rapper thừa nhận tham gia Anh Trai Say Hi vì "cơm áo gạo tiền"?
Tv show
22:29:48 24/09/2025
Phóng pin khỏi xe, thử nghiệm chống cháy ô tô điện gây sốc tại Trung Quốc
Netizen
22:21:51 24/09/2025
 Những học bổng hấp dẫn dành cho sinh viên quốc tế đến Hàn Quốc
Những học bổng hấp dẫn dành cho sinh viên quốc tế đến Hàn Quốc Thầy giáo Lương Trường Xuân có duyên với danh hiệu thủ khoa
Thầy giáo Lương Trường Xuân có duyên với danh hiệu thủ khoa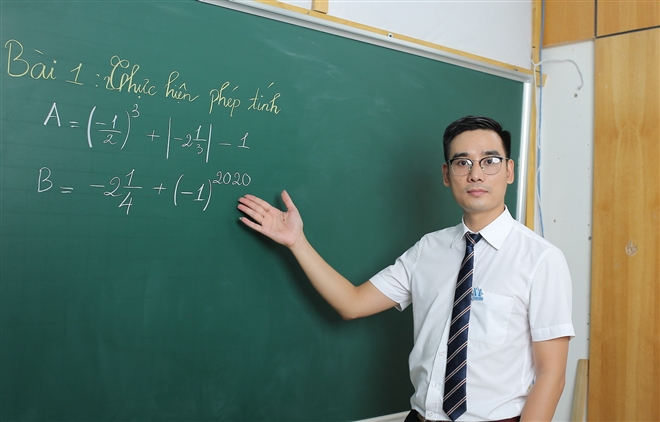

 Ôn thi tốt nghiệp THPT môn Văn: 6 lưu ý quan trọng về Nghị luận văn học
Ôn thi tốt nghiệp THPT môn Văn: 6 lưu ý quan trọng về Nghị luận văn học Cô hiệu trưởng Trường Việt Đức bày "thủ thuật" làm bài thi tiếng Anh vào lớp 10
Cô hiệu trưởng Trường Việt Đức bày "thủ thuật" làm bài thi tiếng Anh vào lớp 10 An toàn và chất lượng
An toàn và chất lượng Thi vào lớp 10 mùa dịch: Giáo viên mách nước cách học để đạt điểm cao
Thi vào lớp 10 mùa dịch: Giáo viên mách nước cách học để đạt điểm cao Thi vào lớp 10: Chiến thuật ôn tập giành điểm cao môn Lịch sử
Thi vào lớp 10: Chiến thuật ôn tập giành điểm cao môn Lịch sử HOCMAI "tiếp sức" 1 triệu khóa học ôn thi trực tuyến trong mùa dịch
HOCMAI "tiếp sức" 1 triệu khóa học ôn thi trực tuyến trong mùa dịch Ôn thi nước rút vào lớp 10: Những lưu ý quan trọng trong môn Ngữ văn
Ôn thi nước rút vào lớp 10: Những lưu ý quan trọng trong môn Ngữ văn


 Yên Bái kích hoạt tình huống học tập chống dịch Covid-19 trong các nhà trường
Yên Bái kích hoạt tình huống học tập chống dịch Covid-19 trong các nhà trường
 Sốc: Hương Giang là đại diện Việt Nam thi Miss Universe 2025!
Sốc: Hương Giang là đại diện Việt Nam thi Miss Universe 2025! Công an cảnh báo thủ đoạn dùng nghệ sĩ quảng cáo cờ bạc
Công an cảnh báo thủ đoạn dùng nghệ sĩ quảng cáo cờ bạc Diện váy 5 triệu đồng ra mắt mẹ bạn trai, tôi cay đắng khi nhận ra bà là ai
Diện váy 5 triệu đồng ra mắt mẹ bạn trai, tôi cay đắng khi nhận ra bà là ai Son Ye Jin - Hyun Bin sắp lên chức bố mẹ lần nữa?
Son Ye Jin - Hyun Bin sắp lên chức bố mẹ lần nữa?
 Thuyết âm mưu bủa vây showbiz Trung Quốc
Thuyết âm mưu bủa vây showbiz Trung Quốc Loạt thị phi của Ưng Hoàng Phúc - Khánh Phương: Từ ồn ào từ thiện, bán "chui" cổ phiếu đến quảng cáo cá độ
Loạt thị phi của Ưng Hoàng Phúc - Khánh Phương: Từ ồn ào từ thiện, bán "chui" cổ phiếu đến quảng cáo cá độ Song Seung Hun và lời chia sẻ cảm động dành cho mẹ
Song Seung Hun và lời chia sẻ cảm động dành cho mẹ Lá thư xúc động bố ca sĩ Đức Phúc gửi Mỹ Tâm và Hồ Hoài Anh
Lá thư xúc động bố ca sĩ Đức Phúc gửi Mỹ Tâm và Hồ Hoài Anh Hoá ra vai chính Mưa Đỏ vốn là của mỹ nam Tử Chiến Trên Không: Biết danh tính ai cũng sốc, lý do từ chối quá đau lòng
Hoá ra vai chính Mưa Đỏ vốn là của mỹ nam Tử Chiến Trên Không: Biết danh tính ai cũng sốc, lý do từ chối quá đau lòng Khó cứu Jeon Ji Hyun: Mất trắng 854 tỷ sau 1 đêm, bị công ty quản lý "mang con bỏ chợ"
Khó cứu Jeon Ji Hyun: Mất trắng 854 tỷ sau 1 đêm, bị công ty quản lý "mang con bỏ chợ" Sự thật về vụ tự tử của người phụ nữ bán rau bị cướp điện thoại
Sự thật về vụ tự tử của người phụ nữ bán rau bị cướp điện thoại Chưa thấy phu nhân tài phiệt nào kém sang thế này: Nhan sắc sến súa lạc quẻ, giọng nói còn tuyệt vọng hơn
Chưa thấy phu nhân tài phiệt nào kém sang thế này: Nhan sắc sến súa lạc quẻ, giọng nói còn tuyệt vọng hơn Bé gái sơ sinh bị bỏ ở trạm điện cùng tờ giấy ghi tên và 15 triệu đồng
Bé gái sơ sinh bị bỏ ở trạm điện cùng tờ giấy ghi tên và 15 triệu đồng Chàng trai yêu thầm mẹ của bạn học và cái kết viên mãn sau nhiều năm
Chàng trai yêu thầm mẹ của bạn học và cái kết viên mãn sau nhiều năm Lời khai của nghi phạm vụ người phụ nữ tử vong sau khi bị cướp điện thoại
Lời khai của nghi phạm vụ người phụ nữ tử vong sau khi bị cướp điện thoại Vợ cũ tiết lộ thông tin bất ngờ về cuộc sống của ông Minh - bà Giao sau khi nhận hơn 1,5 tỷ từ mạnh thường quân
Vợ cũ tiết lộ thông tin bất ngờ về cuộc sống của ông Minh - bà Giao sau khi nhận hơn 1,5 tỷ từ mạnh thường quân Ưng Hoàng Phúc đã có mặt để làm việc với Công an TP.HCM theo thư triệu tập
Ưng Hoàng Phúc đã có mặt để làm việc với Công an TP.HCM theo thư triệu tập