Lưu ý khi ôn tập hình học giải tích trong không gian
Thầy Trần Thế Hùng (trường THPT Chuyên Hà Tĩnh) chia sẻ cách ôn tập để làm những câu hình học giải tích trong không gian khi thi Toán tốt nghiệp THPT.
Chủ đề Hình học giải tích trong không gian chiếm 8 câu hỏi trong đề minh họa thi tốt nghiệp THPT do Bộ Giáo dục và Đào tạo công bố, bao quát hầu hết chủ điểm với đầy đủ mức độ nhận biết, thông hiểu, vận dụng, vận dụng cao. So với năm 2020, chủ đề này được quan tâm nhiều hơn về cả số lượng và mức độ.
Với nội dung ở mức độ nhận biết, thông hiểu, các câu hỏi về tọa độ trong không gian luôn khá cơ bản, chẳng hạn xác định tọa độ hình chiếu vuông góc của một điểm lên các trục tọa độ, mặt phẳng tọa độ, hay xác định tọa độ trung điểm của một đoạn thẳng, tọa độ trọng tâm của một tam giác.
Để giải quyết được những câu hỏi phần này, yêu cầu cần thiết đối với học sinh là nắm vững công thức và cẩn thận đọc kỹ đề, tránh nhầm lẫn nội dung câu hỏi giữa các trục tọa độ hay mặt phẳng tọa độ.
Thầy Trần Thế Hùng từng bỏ dở Đại học Y Hà Nội để theo học Sư phạm Toán. Ảnh: Nhân vật cung cấp.
Phương trình mặt phẳng được đề cập với một câu hỏi trong đề minh họa, tuy nhiên đây là nội dung quan trọng với khá nhiều dạng toán quen thuộc như chỉ ra véc-tơ pháp tuyến của mặt phẳng, xác định điểm mà mặt phẳng đi qua, phương trình mặt phẳng đoạn chắn, mặt phẳng trung trực của đoạn thẳng… Ngoài ra, các dạng toán khác học sinh cũng nên nhớ gồm lập phương trình mặt phẳng với yếu tố song song, vuông góc hay các bài toán liên quan đến góc, khoảng cách.
So với phương trình mặt phẳng, nội dung về phương trình đường thẳng được đề cập nhiều hơn. Học sinh cần lưu ý các dạng toán quen thuộc từ cơ bản đến vận dụng như: Chỉ ra véc-tơ chỉ phương, chỉ ra điểm thuộc đường thẳng, lập phương trình đường thẳng qua hai điểm, phương trình đường thẳng song song, vuông góc.
Video đang HOT
Các em cũng không thể bỏ qua các bài toán có yếu tố tương giao, đường thẳng cắt đường thẳng, đường thẳng cắt mặt phẳng. Đây là một nội dung từng xuất hiện trong đề 2018 và được đề cập lại trong đề minh họa năm nay. Đối với bài toán này, phương pháp chung là gọi tọa độ điểm cắt theo tham số, sau đó tiến hành giải quyết từng bước theo giả thiết bài toán. Hãy cùng xét câu 45 trong đề minh họa 2021 kèm với lời giải dưới đây:
Phương trình mặt cầu là nội dung được quan tâm với 3 câu hỏi trong đề minh họa, trong đó có một câu hỏi vận dụng cao kết hợp nhiều nét mới, tổng hợp nhiều phần kiến thức như khối tròn xoay, giá trị lớn nhất – nhỏ nhất, hình giải tích Oxyz.
Nội dung câu hỏi cơ bản vẫn xoay quanh các dạng toán quen thuộc mà các em cần chú ý rèn luyện như: Xác định tâm, bán kính mặt cầu, lập phương trình mặt cầu biết tâm và bán kính, biết tâm và điểm đi qua, mặt cầu tiếp xúc mặt phẳng, đường thẳng, mặt cầu nhận đoạn thẳng làm đường kính…
Các bài toán khó hơn có thể hỏi nội dung liên quan đến tương giao giữa mặt cầu và đường thẳng, mặt phẳng, xét điểm trên mặt cầu hay liên quan đến cực trị. Các em có thể tham khảo một số câu hỏi vận dụng cao phần này với nội dung và mức độ tương đương trong một số đề thi thử của các trường chuyên trên toàn quốc như câu 42 trong đề do trường THPT chuyên Thái Bình ra hay câu 49 trong đề của trường THPT chuyên Lương Văn Chánh – Phú Yên:
Như vậy, trong 5 ngày qua, thầy đã chỉ ra những định hướng cơ bản giúp các em có một cái nhìn tổng quát cũng như trọng tâm nhất về từng chủ đề trong đề thi tốt nghiệp THPT môn Toán. Hy vọng các em sẽ ôn tập một cách hiệu quả.
Giành điểm tối đa bài hình học không gian đề thi tốt nghiệp THPT
Thầy Trần Thế Hùng, trường THPT chuyên Hà Tĩnh, cho rằng hình học không gian là nội dung dễ kiếm điểm nên học sinh cần chú ý ôn tập.
Hình học không gian cổ điển là chủ đề trọng tâm trong chương trình Toán THPT, học sinh được học xuyên suốt từ lớp 11 đến lớp 12. Phân tích đề minh họa thi tốt nghiệp THPT của Bộ Giáo dục và Đào tạo, có thể thấy có 7 câu hỏi liên quan đến chủ đề này, phân bổ trên các mức độ nhận biết, thông hiểu, vận dụng, là nội dung cơ bản và khá dễ kiếm điểm đối với học sinh.
Với các bài toán về khối đa diện và thể tích khối đa diện , để làm tốt những câu hỏi nhận biết và thông hiểu, học sinh cần nắm vững công thức tính thể tích khối chóp, khối lăng trụ. Các em cũng cần tập trung xử lý các hình cơ bản, trường hợp đặc biệt như khối chóp đều, khối chóp có ba cạnh đôi một vuông góc, khối chóp có cạnh bên, mặt bên vuông góc với đáy, hình lăng trụ đều, hình hộp chữ nhật, hình lập phương...
Để giải quyết các câu vận dụng và vận dụng cao, học sinh cần tư duy tổng hợp cũng như xử lý tốt yếu tố về góc và khoảng cách đi kèm trong bài toán thể tích.
Thầy Trần Thế Hùng là giáo viên Toán của trường THPT chuyên Hà Tĩnh. Ảnh: Nhân vật cung cấp.
Một chủ đề khác là bài toán liên quan đến tỷ số thể tích , tuy chưa xuất hiện trong đề minh họa năm nay nhưng có trong đề những năm trước. Đây là dạng toán khó cần vận dụng tốt kỹ năng hình học tổng hợp, phân cắt và chia hình cũng như cần khéo léo vận dụng phương pháp đặc biệt hóa bài toán, tọa độ hóa để giải quyết một cách hiệu quả. Ví dụ câu 47 trong đề thi THPT quốc gia năm 2019:
Bài toán này đòi hỏi sự khéo léo trong phân chia khối đa diện thành các khối nhỏ, sau đó sử dụng công thức tỷ số thể tích để tính. Học sinh cũng có thể đặc biệt hóa bài toán thành lăng trụ đứng kết hợp với tọa độ hóa để giải quyết.
Về các bài toán liên quan đến khối tròn xoay , có lẽ yêu cầu nhẹ nhàng hơn với đa số học sinh khi chỉ cần nhớ và vận dụng tốt các công thức có sẵn cũng như phân biệt chính xác các khái niệm liên quan.
Một số câu hỏi như câu 38 mã 101 đề năm 2019, câu 35 mã 101 đề năm 2020 lần 1, câu 29 mã 102 đề năm 2020 lần 2 đòi hỏi hiểu rõ bản chất của khái niệm thì mới giải quyết chính xác yêu cầu bài toán.
Với các câu hỏi ở mức độ vận dụng trong dạng bài này, học sinh cần rèn luyện kỹ hơn các bài toán liên quan đến thiết diện, một số câu hỏi về cực trị, thực tế liên quan đến khối tròn xoay.
Một nội dung học từ lớp 11 nhưng không thể không nói đến là bài toán về góc và khoảng cách. Các em cần nắm vững cách xác định góc giữa hai đường thẳng, hai mặt phẳng, đường thẳng và mặt phẳng, từ đó tính toán theo yêu cầu của đề bài.
Đối với bài toán khoảng cách, các em cần có kỹ năng tính toán tốt, lựa chọn cẩn thận giữa tính toán xác định trực tiếp khoảng cách hay tính gián tiếp thông qua yếu tố khác. Chẳng hạn câu 40 mã 101 đề năm 2019, câu 43 đề 101 đề năm 2020 lần 1 khi tính gián tiếp sẽ thuận lợi hơn. Bên cạnh đó, phương pháp tiếp cận bằng tọa độ hóa hơi dài nhưng cũng là giải pháp an toàn cho những bạn chưa nắm vững cách xác định khoảng cách giữa hai đường thẳng chéo nhau.
Lời giải câu 43:
Cuối cùng, một lưu ý tuy nhỏ nhưng cũng rất quan trọng là các em nên tận dụng hình vẽ cho sẵn trên đề và có thể thực hiện các tính toán ngay trên đó để phần nào tiết kiệm thời gian vẽ lại hình.
Hàm số mũ - logarit và các câu đại số lớp 11 trong đề tốt nghiệp  Thầy Trần Thế Hùng (trường THPT Chuyên Hà Tĩnh) chỉ ra những lưu ý giúp thí sinh giành điểm ở hơn 10 câu chủ đề hàm số mũ - logarit hay tổ hợp - xác suất. Phân tích đề thi tốt nghiệp THPT tham khảo được Bộ Giáo dục và Đào tạo công bố cuối tháng 3, chủ đề hàm số mũ -...
Thầy Trần Thế Hùng (trường THPT Chuyên Hà Tĩnh) chỉ ra những lưu ý giúp thí sinh giành điểm ở hơn 10 câu chủ đề hàm số mũ - logarit hay tổ hợp - xác suất. Phân tích đề thi tốt nghiệp THPT tham khảo được Bộ Giáo dục và Đào tạo công bố cuối tháng 3, chủ đề hàm số mũ -...
 Cảnh tượng kinh hoàng khi 4 thuyền du lịch bất ngờ lật úp, 84 người cùng rơi xuống sông00:37
Cảnh tượng kinh hoàng khi 4 thuyền du lịch bất ngờ lật úp, 84 người cùng rơi xuống sông00:37 Bí Đỏ tả thực cuộc sống với Vũ Cát Tường, netizen xót: Thương Tường quá, nhưng kệ nha...00:30
Bí Đỏ tả thực cuộc sống với Vũ Cát Tường, netizen xót: Thương Tường quá, nhưng kệ nha...00:30 Thiếu gia tập đoàn nổi tiếng cả nước phải "nín thở" khi đi ăn với vợ00:18
Thiếu gia tập đoàn nổi tiếng cả nước phải "nín thở" khi đi ăn với vợ00:18 Hình ảnh lạ của những chú ngựa trong dàn kỵ binh sau khi hoàn thành nhiệm vụ đại lễ 30/401:17
Hình ảnh lạ của những chú ngựa trong dàn kỵ binh sau khi hoàn thành nhiệm vụ đại lễ 30/401:17 Cứ ngỡ sản phẩm của AI nhưng hình ảnh "em bé cưỡi hổ" trong xóm nhỏ TP.HCM là ảnh thật: Câu chuyện phía sau mới thú vị!01:35
Cứ ngỡ sản phẩm của AI nhưng hình ảnh "em bé cưỡi hổ" trong xóm nhỏ TP.HCM là ảnh thật: Câu chuyện phía sau mới thú vị!01:35 Xác minh clip tài xế Grab tại Đà Nẵng bị khách đánh tới tấp00:34
Xác minh clip tài xế Grab tại Đà Nẵng bị khách đánh tới tấp00:34 Hóng: Drama gái xinh thay đồ trên xe hút hơn 3 triệu lượt người vào xem00:43
Hóng: Drama gái xinh thay đồ trên xe hút hơn 3 triệu lượt người vào xem00:43 Sự đối lập trong bữa cơm của bố qua camera khiến con gái xem xong thấy bất lực, nước mắt chảy dài00:19
Sự đối lập trong bữa cơm của bố qua camera khiến con gái xem xong thấy bất lực, nước mắt chảy dài00:19 Không ai còn nhận ra con gái thứ 2 của Quyền Linh00:16
Không ai còn nhận ra con gái thứ 2 của Quyền Linh00:16 Luật sư Hà 'bị réo' tham vấn luật nổi nhất 'Tóp tóp' lộ quá khứ bán cá ít ai ngờ06:06
Luật sư Hà 'bị réo' tham vấn luật nổi nhất 'Tóp tóp' lộ quá khứ bán cá ít ai ngờ06:06 Chu Thanh Huyền ngồi xế hộp bạc tỷ hậu drama, chứng minh 'ăn đứt' vợ bạn chồng03:17
Chu Thanh Huyền ngồi xế hộp bạc tỷ hậu drama, chứng minh 'ăn đứt' vợ bạn chồng03:17Tin đang nóng
Tin mới nhất

Còn nhiều băn khoăn về chứng nhận giỏi cấp tỉnh với học sinh điểm IELTS cao

Việc thực hiện chương trình, SGK mới còn nhiều khó khăn

Cấp phép tổ chức thi chứng chỉ HSK trở lại

Banner tìm hiểu ngày 22/12 của Trường ĐH Tôn Đức Thắng in hình lính Mỹ

Nhiều tỉnh cho học sinh nghỉ Tết hơn 10 ngày, Hà Nội lý giải nghỉ 8 ngày

Trường ĐH Kiên Giang dự kiến tuyển hơn 1.600 chỉ tiêu năm 2023

Trường Đại học Hồng Đức nâng cao chất lượng đào tạo sinh viên ngành giáo dục mầm non

Học sinh Hà Giang nghỉ Tết Quý Mão 12 ngày, từ 27 tháng Chạp

Nhiều tiết dạy sáng tạo tại hội thi giáo viên dạy giỏi Hà Nội

Trường Đại học Kinh tế Quốc dân công bố Đề án tuyển sinh đại học năm 2023

Tuyển sinh 2023: Đại học Kinh tế Quốc dân công bố đề án tuyển sinh

Cần cẩn trọng lựa chọn nhân sự, ra đề thi
Có thể bạn quan tâm

Võ Hạ Trâm giảm 19kg sau khi sinh, sắc vóc quyến rũ tuổi 35
Sao việt
21:38:54 09/05/2025
Ngoài 50 tuổi, nên uống 4 tách cà phê mỗi ngày
Sức khỏe
21:37:42 09/05/2025
Quốc Huy - Nam diễn viên điển trai trong "Người vợ cuối cùng" và "Thám tử Kiên"
Hậu trường phim
21:35:58 09/05/2025
Tôi có 20 tỷ đồng nên muốn về hưu non, nhưng vợ bắt làm việc đến 60 tuổi
Góc tâm tình
21:32:49 09/05/2025
Raul Rocha: Tỷ phú Mexico sở hữu Hoa hậu Hoàn Vũ, bắt tay Nawat làm loạn là ai?
Tin nổi bật
21:31:37 09/05/2025
Ngọc Huyền và Trần Nghĩa bị phản ứng trong "Cha tôi, người ở lại"
Phim việt
21:31:08 09/05/2025
Tàu hải quân Philippines, Trung Quốc đối đầu gần bãi cạn Scarborough ở Biển Đông
Thế giới
21:19:26 09/05/2025
Cung Tuyết Hoa: Hoa hậu ở tù vì bạn trai, 28 năm không gần đàn ông, U80 độc thân
Sao châu á
21:17:28 09/05/2025
Giải pháp giảm mỡ bụng nhanh nhất
Làm đẹp
21:12:06 09/05/2025
Kylie Jenner lần đầu đi thảm đỏ với Timothée Chalamet, "quê xệ" vì 1 điều
Sao âu mỹ
21:07:43 09/05/2025
 Cách chinh phục hai đại học top đầu thế giới
Cách chinh phục hai đại học top đầu thế giới 10 trường kinh doanh có tỷ lệ chấp nhận thấp nhất nước Mỹ
10 trường kinh doanh có tỷ lệ chấp nhận thấp nhất nước Mỹ






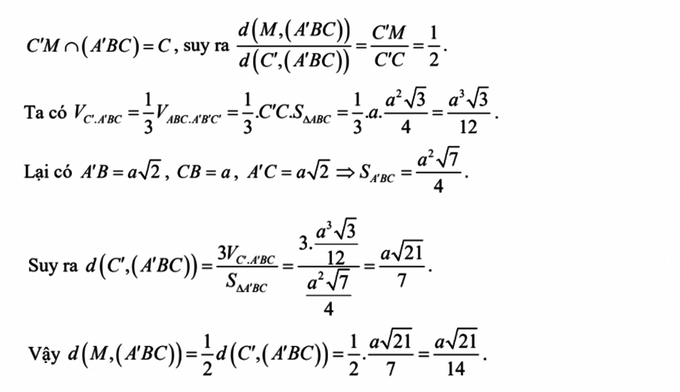
 Các dạng bài đạo hàm và ứng dụng trong đề Toán tốt nghiệp THPT
Các dạng bài đạo hàm và ứng dụng trong đề Toán tốt nghiệp THPT Hàm số mũ: Những kiến thức không thể bỏ qua
Hàm số mũ: Những kiến thức không thể bỏ qua
 Bí quyết làm nguyên hàm - tích phân trong đề tốt nghiệp THPT
Bí quyết làm nguyên hàm - tích phân trong đề tốt nghiệp THPT Bí quyết ôn thi tốt nghiệp THPT đạt điểm cao môn toán: Tích phân
Bí quyết ôn thi tốt nghiệp THPT đạt điểm cao môn toán: Tích phân Thầy giáo 'mách nước' ôn thi tốt nghiệp THPT 2021 môn Toán giành điểm cao
Thầy giáo 'mách nước' ôn thi tốt nghiệp THPT 2021 môn Toán giành điểm cao Giúp sĩ tử chinh phục phần nguyên hàm và tích phân trong môn Toán
Giúp sĩ tử chinh phục phần nguyên hàm và tích phân trong môn Toán Bí quyết ôn thi THPT đạt điểm cao môn toán: Phương trình mặt phẳng
Bí quyết ôn thi THPT đạt điểm cao môn toán: Phương trình mặt phẳng

 Cách ôn thi THPT môn sinh hiệu quả
Cách ôn thi THPT môn sinh hiệu quả
 Máy bay Vietjet Air trượt khỏi đường băng khi hạ cánh
Máy bay Vietjet Air trượt khỏi đường băng khi hạ cánh Nóng: Won Bin chính thức lên tiếng sau bao lần bị réo gọi vào scandal chấn động của Kim Soo Hyun
Nóng: Won Bin chính thức lên tiếng sau bao lần bị réo gọi vào scandal chấn động của Kim Soo Hyun Á hậu 10 năm dẫn Thời sự VTV: Là mỹ nhân có tiếng Hà Nội, ai cũng mê
Á hậu 10 năm dẫn Thời sự VTV: Là mỹ nhân có tiếng Hà Nội, ai cũng mê Lấy chồng họ lạ, bà mẹ Quảng Ngãi 'vắt óc' đặt tên con, gặp bao chuyện hài hước
Lấy chồng họ lạ, bà mẹ Quảng Ngãi 'vắt óc' đặt tên con, gặp bao chuyện hài hước Hoa hậu Việt bị nghi mang bầu giả tiếp tục đáp trả căng ngay trên sóng livestream
Hoa hậu Việt bị nghi mang bầu giả tiếp tục đáp trả căng ngay trên sóng livestream Hoa hậu Ý Nhi được Miss World ưu ái, độ hot chỉ xếp sau đối thủ đặc biệt này
Hoa hậu Ý Nhi được Miss World ưu ái, độ hot chỉ xếp sau đối thủ đặc biệt này Lôi ra loạt váy vóc trong vali của cụ ông U80 "phượt" xe máy từ Nghệ An vào TP.HCM: Có lý do đặc biệt
Lôi ra loạt váy vóc trong vali của cụ ông U80 "phượt" xe máy từ Nghệ An vào TP.HCM: Có lý do đặc biệt Tổng thống Nga tuyên bố tiếp tục chống chủ nghĩa phát xít
Tổng thống Nga tuyên bố tiếp tục chống chủ nghĩa phát xít Nam hiệu trưởng 'trượt tay' gửi ảnh, group trường 27 người 'rửa mắt', lý do sốc!
Nam hiệu trưởng 'trượt tay' gửi ảnh, group trường 27 người 'rửa mắt', lý do sốc!
 Công bố kết luận giám định vụ tai nạn khiến nữ sinh tử vong ở Vĩnh Long
Công bố kết luận giám định vụ tai nạn khiến nữ sinh tử vong ở Vĩnh Long
 Đại học Văn Lang đưa ra quyết định cuối cùng với nam sinh vô lễ với Cựu chiến binh
Đại học Văn Lang đưa ra quyết định cuối cùng với nam sinh vô lễ với Cựu chiến binh Phát hiện 50kg vàng và 10 tỷ đồng tiền mặt trong phòng trọ 20m2
Phát hiện 50kg vàng và 10 tỷ đồng tiền mặt trong phòng trọ 20m2
 Nam thần Vbiz nhận cát-xê tới 60 cây vàng: Giải nghệ sớm, từng nặng tới gần 130kg
Nam thần Vbiz nhận cát-xê tới 60 cây vàng: Giải nghệ sớm, từng nặng tới gần 130kg Nghệ sĩ đặc biệt nhất showbiz Việt: 2 lần kết hôn, 1 lần cưới vợ, 1 lần lấy chồng, U40 đi thi hoa hậu
Nghệ sĩ đặc biệt nhất showbiz Việt: 2 lần kết hôn, 1 lần cưới vợ, 1 lần lấy chồng, U40 đi thi hoa hậu "Hoa hậu lùn nhất Việt Nam" rút lui khỏi showbiz hậu lấy chồng Tiến sĩ, biệt thự trải dài khắp cả nước
"Hoa hậu lùn nhất Việt Nam" rút lui khỏi showbiz hậu lấy chồng Tiến sĩ, biệt thự trải dài khắp cả nước