Lộ diện tác giả đề Toán lớp 2 khiến người lớn đầu hàng
Bài toán “đầu cừu, đuôi thuyền trưởng” có nguồn gốc khá thú vị.
Những ngày qua cộng đồng mạng xôn xao về đề Toán lớp 2, đếm cừu tính tuổi thuyền trưởng. Thực tế, đây là một bài toán nghiêm túc và tác giả của nó chính là nhà giáo ưu tú Phạm Đình Thực – Nguyên trưởng bộ môn phương pháp dạy Toán tiểu học của trường ĐH Sài Gòn.
Nhà giáo ưu tú Phạm Đình Thực cho biết, cách ra đề kiểu này không phải là mới, lạ với thế giới. Vì đối với những người dạy học Toán, bài toán “Tuổi thuyền trưởng” đã trở thành kinh điển, không ai không biết.
Bài toán như sau: “Trên tàu có 45 con cừu, 5 con bị rơi xuống nước. Hỏi ông thuyền trưởng bao nhiêu tuổi?”.
Bên cạnh đó, nếu chú ý, có thể thấy bài toán được đánh dấu (*) – tức là bài toán khó nhằm mục đích nâng cao năng lực nhận thức và kĩ năng phát hiện vấn đề của học sinh, đồng thời rèn luyện kĩ năng đọc kĩ đề và suy nghĩ thấu đáo trước khi làm bài.
“Thường để cho yên tâm và an toàn, cả tác giả và Nhà xuất bản ở Việt Nam ít khi mạnh dạn chấp nhận kiểu đề toán ra theo dạng này. Nhưng, theo quan điểm đổi mới giáo dục của Đảng và của Bộ GD&ĐT, tôi đã đề nghị nhà xuất bản chấp nhận ra đề kiểu này và tôi đã được ủng hộ.
Người ra đề Toán tìm tuổi thuyền trưởng.
Trong một bài toán có 2 phần là những cái đã cho và cái phải tìm. Câu hỏi này không đúng vì trong các dữ kiện không có yếu tố nào liên quan đến tuổi thuyền trưởng. Tác giả cố tình vi phạm để tập cho trẻ thói quen đọc kỹ đề, phân biệt cái đã cho và cái phải tìm trước khi giải bài toán.
Cũng xin lưu ý thêm rằng, trong sách bên cạnh câu hỏi còn có phần gợi ý giải; và đáp án bài toán này trong sách có ghi rõ là: “Không giải được vì đề toán sai” – Nhà giáo Ưu tú Phạm Đình Thực bày tỏ.
Hiện nay, thực hiện công cuộc đổi mới căn bản, toàn diện GD&ĐT, một nhiệm vụ quan trọng hàng đầu là phải đổi mới tư duy, trước hết là tư duy viết sách giáo khoa, sách tham khảo đáp ứng được yêu cầu nâng cao năng lực của học sinh. Bên cạnh đó, kiểm tra, đánh giá được coi là khâu đột phá trong công cuộc đổi mới GD&ĐT lần này.
Từ hiện tượng bài toán lớp 2 gây tranh cãi, cho thấy phần nhiều độc giả thể hiện quan điểm ủng hộ việc đã đến lúc chúng ta không thể theo thói quen cũ bắt học sinh chỉ có một lựa chọn thuần nhất, thụ động trong việc tiếp nhận tri thức.
Với trường hợp cụ thể này, theo lẽ thông thường, trước khi tranh luận, chúng ta nên trấn tĩnh, chí ít là tìm xem trong cuốn sách đó có phần đáp án không, và đáp án trả lời thế nào rồi sau mới bàn.
Theo Hiếu Nguyễn/Giáo dục Thời đại
15 sai lầm thường gặp khi làm bài thi môn Toán
Thạc sĩ Nguyễn Sơn Hà - giáo viên trường THPT chuyên Đại học Sư phạm Hà Nội - cho biết: Để không bị mất điểm môn Toán kì thi ĐH, học sinh cần chú ý:
1. Biến đổi "tương đương" trong những tình huống chỉ đúng một chiều là chiều "suy ra"
Những biến đổi sau không đúng:
Video đang HOT
Hai đường thẳng song song "tương đương" với hai hệ số góc bằng nhau.
Đường thẳng d vuông góc với mặt phẳng ABC &'tương đương' đường thẳng d vuông góc với đường thẳng AB.
f(x) bằng g(x) &'tương đương' với đạo hàm của f(x) bằng đạo hàm của g(x).
u bằng f(x) &'tương đương' với du bằng đạo hàm của f(x) nhân với dx.
Hệ hai phương trình f(x,y)=0 và g(x,y)=0 &'tương đương' với một phương trình a.f(x,y) b.g(x,y)=0 (a, b là hai số thực khác 0).
Hai số phức bằng nhau &'tương đương' với hai phần thực bằng nhau.
Hai số phức bằng nhau &'tương đương' với hai phần ảo bằng nhau....
Giải pháp an toàn: Một số trường hợp thường dùng biến đổi "tương đương" là giải phương trình, giải hệ phương trình, giải bất phương trình, giải hệ bất phương trình, giải bài toán tìm điều kiện cần và đủ. Các trường hợp khác, học sinh nên biến đổi "suy ra".
Tóm lại, khi khẳng định &'Nếu A thì B' đúng và khẳng định "Nếu B thì A" sai, học sinh không được biến đổi "tương đương".
2. Thiếu điều kiện, thừa kết quả, quên kết luận
Khi bài toán có biểu thức căn bậc hai, biểu thức có ẩn dưới mẫu số, biểu thức tanx, biểu thức cotx, biểu thức logarit, dạng đại số của số phức, học sinh cần hình thành &'phản xạ có điều kiện' và kiểm tra lại điều kiện trước khi viết đáp số.
Với những bài toán cần xét nhiều trường hợp, học sinh cần chú ý tổng hợp kết quả và kết luận.
3. Gạch đầu dòng tùy tiện
Nếu học sinh gạch đầu dòng liền trước một biểu thức thì có thể bị hiểu là: nhầm dấu của biểu thức
Ví dụ: Giải phương trình sinx cosx = 1. Nếu học sinh gạch đầu dòng l
" - sinx cosx = 1"
thì sẽ bị hiểu nhầm là &'biểu thức trừ sinx cộng với cosx bằng 1'.
4. Viết lời giải bài toán như một &'đoạn văn' dài, không chia ý rõ ràng và làm sai ở câu cuối cùng của đoạn mình viết
Học sinh nên chia ý rõ ràng và xuống dòng khi kết thúc các ý, nếu sai ý sau thì vẫn được chấm điểm ý trước.
Mỗi bài toán thi đại học thường được tính 1 điểm và đáp án thường có 4 ý, mỗi ý 0,25 điểm. Các học sinh cần chú ý điều này để trình bày các ý rõ ràng.
5. Viết nhầm lẫn các chữ, các kí hiệu
Học sinh chú ý phân biệt các chữ, các kí hiệu sau khi viết bài thi:
Chữ i và số 1, chữ b và số 6, chữ z và số 2, chữ D và chữ P, chữ D và chữ O, chữ P và chữ O, chữ H và chữ A, chữ g và chữ y, chữ g và chữ q, chữ q và số 9, chữ C và dấu ngoặc đơn ( , chữ C và kí hiệu chỉ quan hệ tập hợp con, dấu ngoặc đơn ( và kí hiệu chỉ quan hệ tập hợp con, chữ u và chữ v, chữ u và chữ n, dùng chung kí hiệu chỉ quan hệ tập hợp con và kí hiệu chỉ quan hệ phần tử thuộc tập hợp, chữ a và kí hiệu góc anpha.
6. Dùng chung tên điểm tại hai vị trí khác nhau
Bài toán phương pháp tọa độ, học sinh thường có thói quen gọi tâm đường tròn là O, gọi tâm mặt cầu là O. Các em cần chú ý rằng, O là gốc tọa độ. Trong trường hợp dùng chung tên điểm, các em không nên vội vàng xóa, có thể khắc phục nhanh sự cố bằng cách thêm dấu phẩy vào điểm đó, ví dụ O'.
7. Tính toán sai, sử dụng kết quả sai để làm tiếp
Học sinh cần chú ý cẩn thận trong từng phép tính, tránh tình trạng tính toán vội vàng rất nhiều phép tính rồi mới kiểm tra từ đầu và sửa sai từ đầu.
8. Lập phương trình sai, sử dụng máy tính để tìm chính xác nghiệm của phương trình đó và yên tâm kết luận
Học sinh cần chú ý kiểm tra kĩ phương trình trước khi dùng máy tính để tìm nghiệm, tránh tình trạng quá tin tưởng máy tính mà quên mất là phương trình sai.
9. Nhập sai số liệu vào máy tính điện tử và yên tâm dùng kết quả của máy tính
Học sinh không nên chủ quan khi dùng máy tính, cần kiểm tra cẩn thận các số liệu khi nhập vào máy tính.
10. Sử dụng máy tính điện tử để tìm nghiệm dưới dạng gần đúng
Khi đáp số được viết dưới dạng phân số hoặc dạng căn bậc hai, dạng logarit của một số dương, nếu máy tính cho kết quả là một số thập phân gần đúng thì vẫn không được chấp nhận với bài toán yêu cầu tìm đúng kết quả. Học sinh cần chú ý thử máy tính trước khi đi thi.
11. Đọc nhầm đề dẫn đến một bài toán dễ hơn, tính toán nhanh hơn, giải được bài toán mới và yên tâm không kiểm tra lại đề bài
Học sinh cần đọc đề kĩ, xác định đúng yếu tố đã cho, điều phải tìm, điều phải chứng minh.
12. Sử dụng đúng giả thiết và mất thời gian đưa ra kết quả mới không liên quan gì đến kết luận của bài toán
Học sinh phải rất cảnh giác với những tình huống &'lạc đề', suy luận đúng nhưng không để làm gì, không phục vụ cho việc giải bài toán trong đề thi.
13. Mất thời gian làm đúng một bài toán không liên quan đến bài toán trong đề thi
Tình huống có thể xảy ra với học sinh và không có điểm.
Bài toán trong đề thi: Chứng minh biểu thức A lớn hơn biểu thức B. Học sinh mất thời gian chứng minh được biểu thức A lớn hơn biểu thức C nhưng
không biết biểu thức C lại nhỏ hơn biểu thức B.
14. Sử dụng kết quả không được quy định trong chương trình
Kết quả được sử dụng để giải bài thi phải phù hợp với sách giáo khoa chương trình hiện hành. Khi học sinh thừa nhận kiến thức không được quy định trong chương trình, học sinh làm đúng, bài thi vẫn không được tính điểm tối đa.
Nếu các học sinh giỏi sử dụng kết quả ngoài sách giáo khoa thì phải chứng minh lại các kết quả đó bằng kiến thức trong sách giáo khoa.
Khi chọn đề theo chương trình ban cơ bản, học sinh đã học sách giáo khoa ban nâng cao có thể không biết những kết quả mình sử dụng không có trong sách giáo khoa ban cơ bản. Học sinh cần tìm hiểu trước những kiến thức có trong sách giáo khoa ban nâng cao nhưng không có trong sách giáo khoa ban cơ bản.
15. Nghĩ được cách giải, học sinh có thể vui mừng và chủ quan, không kiểm soát được mình viết đúng hay viết sai, không cẩn thận trong việc viết kết quả
Học sinh không có cơ hội gặp giám khảo để giải thích suy nghĩ của mình. Khi đi thi, các em không thể bằng lòng sớm với việc phát hiện ra cách giải. Khi ngồi trong phòng thi, yếu tố tâm lí có thể làm cho các em không viết được chính xác những điều đã suy nghĩ.
Học sinh cần chú ý
- Ba yếu tố quan trọng ảnh hưởng đến kết quả thi là: kiến thức, kĩ năng và tâm lí.
- Ba nguyên tắc quan trọng khi viết bài thi để có thể đạt điểm cao là:
3 Đ: Đúng - Đủ - Đẹp.
1) Học sinh phải viết đúng kí hiệu, viết đúng công thức, vẽ hình đúng, lập luận đúng, kết quả đúng.
2) Học sinh phải viết đủ ý.
3) Học sinh phải trình bày đẹp, diễn đạt tốt.
Thạc sĩ Nguyễn Sơn Hà
Theo GDTĐ
Một bài toán lớp 4 hai đáp án sai  Mới đây một bài toán lớp 4 bị phát hiện có đến hai lỗi sai đang khiến rất nhiều phụ huynh bức xúc. Trong một cuốn sách tham khảo của học sinh lớp 4 có bài toán số 3 ngay trên trang 3 của cuốn sách với hai phần a, b và đều đưa sai đáp án. Bài toán lớp 4 với hai...
Mới đây một bài toán lớp 4 bị phát hiện có đến hai lỗi sai đang khiến rất nhiều phụ huynh bức xúc. Trong một cuốn sách tham khảo của học sinh lớp 4 có bài toán số 3 ngay trên trang 3 của cuốn sách với hai phần a, b và đều đưa sai đáp án. Bài toán lớp 4 với hai...
 Clip: Xe bán tải bị đâm nát trên đường tại Sơn La, bé gái trong xe không ngừng hoảng loạn kêu cứu "bố ơi"00:55
Clip: Xe bán tải bị đâm nát trên đường tại Sơn La, bé gái trong xe không ngừng hoảng loạn kêu cứu "bố ơi"00:55 Đoạn camera đau lòng đang được chia sẻ trên MXH: Người phụ nữ bị chồng đánh dã man, các con ôm mẹ gào khóc00:52
Đoạn camera đau lòng đang được chia sẻ trên MXH: Người phụ nữ bị chồng đánh dã man, các con ôm mẹ gào khóc00:52 Phát ngôn về chuyện sao kê của mẹ bé Bắp làm dậy sóng MXH giữa lúc tắt tính năng bình luận01:09
Phát ngôn về chuyện sao kê của mẹ bé Bắp làm dậy sóng MXH giữa lúc tắt tính năng bình luận01:09 Bất bình khi xem clip ghi cảnh cụ bà bị 2 phụ nữ đánh, người vào can còn bị ngăn lại00:38
Bất bình khi xem clip ghi cảnh cụ bà bị 2 phụ nữ đánh, người vào can còn bị ngăn lại00:38 Điếng người trước cảnh tượng bóng trắng di chuyển trong salon tóc lúc 12h đêm02:08
Điếng người trước cảnh tượng bóng trắng di chuyển trong salon tóc lúc 12h đêm02:08Tin đang nóng
Tin mới nhất

Còn nhiều băn khoăn về chứng nhận giỏi cấp tỉnh với học sinh điểm IELTS cao

Việc thực hiện chương trình, SGK mới còn nhiều khó khăn

Cấp phép tổ chức thi chứng chỉ HSK trở lại

Banner tìm hiểu ngày 22/12 của Trường ĐH Tôn Đức Thắng in hình lính Mỹ

Nhiều tỉnh cho học sinh nghỉ Tết hơn 10 ngày, Hà Nội lý giải nghỉ 8 ngày

Trường ĐH Kiên Giang dự kiến tuyển hơn 1.600 chỉ tiêu năm 2023

Trường Đại học Hồng Đức nâng cao chất lượng đào tạo sinh viên ngành giáo dục mầm non

Học sinh Hà Giang nghỉ Tết Quý Mão 12 ngày, từ 27 tháng Chạp

Nhiều tiết dạy sáng tạo tại hội thi giáo viên dạy giỏi Hà Nội

Trường Đại học Kinh tế Quốc dân công bố Đề án tuyển sinh đại học năm 2023

Tuyển sinh 2023: Đại học Kinh tế Quốc dân công bố đề án tuyển sinh

Cần cẩn trọng lựa chọn nhân sự, ra đề thi
Có thể bạn quan tâm
WHO duy trì tình trạng khẩn cấp y tế toàn cầu đối với bệnh đậu mùa khỉ
Thế giới
05:34:00 28/02/2025
Cẩn thận với hội chứng người đỏ do thuốc
Sức khỏe
04:35:03 28/02/2025
Bắt đối tượng xúc phạm người khác trên mạng xã hội
Pháp luật
00:00:05 28/02/2025
Bộ phim 18+ nóng bỏng nhất sự nghiệp của mỹ nhân Gossip Girl vừa qua đời
Hậu trường phim
23:49:32 27/02/2025
Ngoại hình gây hoang mang tột độ của Tiểu Long Nữ đẹp nhất màn ảnh
Sao châu á
23:44:29 27/02/2025
Phim Hàn hay đến mức rating tăng 132% chỉ sau 1 tập, nữ chính đã đẹp mê mẩn còn có cảnh nóng cực cháy
Phim châu á
23:41:43 27/02/2025
4 phim 18+ nóng bỏng mắt của "mỹ nhân đẹp nhất thế kỷ": Hàng cổ đánh đổ dân chơi
Phim âu mỹ
23:37:36 27/02/2025
Ronaldo khiến mạng xã hội bùng nổ
Sao thể thao
23:34:58 27/02/2025
Jennie nói 1 câu khiến tất cả những kẻ thù ghét "nín họng"
Nhạc quốc tế
23:28:53 27/02/2025
Bí ẩn chưa có lời giải của sao nữ Vbiz sau gần 2 năm sinh đôi và lấy chồng Hàn Quốc
Sao việt
23:25:36 27/02/2025
 Tuyển sinh ĐH – CĐ năm 2014: Sẵn sàng cho kỳ thi
Tuyển sinh ĐH – CĐ năm 2014: Sẵn sàng cho kỳ thi Vì sao học sinh thờ ơ với ngành Sư phạm?
Vì sao học sinh thờ ơ với ngành Sư phạm?


 Bài toán '3 - ?=4" khiến phụ huynh cũng bó tay
Bài toán '3 - ?=4" khiến phụ huynh cũng bó tay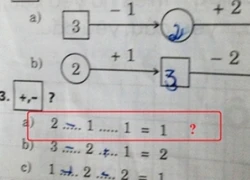 Bài toán lớp 1 cộng trừ khiến học sinh đau đầu
Bài toán lớp 1 cộng trừ khiến học sinh đau đầu Thêm đề toán và đáp án xôn xao cộng đồng mạng
Thêm đề toán và đáp án xôn xao cộng đồng mạng Truy tìm bài toán rợn người
Truy tìm bài toán rợn người Những bài Toán khiến học sinh 'đau đầu'
Những bài Toán khiến học sinh 'đau đầu' Nữ nghệ sĩ đình đám đã bán nốt biệt thự 70 tỷ ở Việt Nam
Nữ nghệ sĩ đình đám đã bán nốt biệt thự 70 tỷ ở Việt Nam Mẹ bé Bắp: 'Ba mẹ ở quê đi chợ mua đồ nhưng không ai bán, nhà có gì ăn nấy'
Mẹ bé Bắp: 'Ba mẹ ở quê đi chợ mua đồ nhưng không ai bán, nhà có gì ăn nấy' Nóng: Báo Hàn "bắt gọn" Lee Jong Suk hẹn hò Moon Ga Young, chuyện tình với IU đã toang?
Nóng: Báo Hàn "bắt gọn" Lee Jong Suk hẹn hò Moon Ga Young, chuyện tình với IU đã toang? Nam nghệ sĩ hài nổi danh cả nước: Tuổi ngoài 60 siêu giàu, gọi vợ là "nữ hoàng cai tù ngọt ngào"
Nam nghệ sĩ hài nổi danh cả nước: Tuổi ngoài 60 siêu giàu, gọi vợ là "nữ hoàng cai tù ngọt ngào" Vợ Yoo Jae Suk phát hiện chồng biểu hiện bất thường, vội phóng về nhà lao thẳng vào phòng ngủ thấy cảnh tượng khó tin
Vợ Yoo Jae Suk phát hiện chồng biểu hiện bất thường, vội phóng về nhà lao thẳng vào phòng ngủ thấy cảnh tượng khó tin Lộ tin nhắn gây ớn lạnh của "nam thần thanh xuân" đang bị điều tra vì dính líu vụ giết người tàn bạo
Lộ tin nhắn gây ớn lạnh của "nam thần thanh xuân" đang bị điều tra vì dính líu vụ giết người tàn bạo Mỹ nhân Việt đổi đời chỉ nhờ 1 cái bĩu môi, cả body lẫn nhan sắc đều thăng hạng đỉnh cao sau 8 năm
Mỹ nhân Việt đổi đời chỉ nhờ 1 cái bĩu môi, cả body lẫn nhan sắc đều thăng hạng đỉnh cao sau 8 năm Cặp đôi nhà sát vách lấy nhau, đám cưới khách ngồi nhầm tiệc, bỏ nhầm phong bì
Cặp đôi nhà sát vách lấy nhau, đám cưới khách ngồi nhầm tiệc, bỏ nhầm phong bì So sánh nhan sắc Lâm Tâm Như ở tuổi 49 mới hiểu thế nào là sự khác biệt của lão hoá nhân tạo và tự nhiên
So sánh nhan sắc Lâm Tâm Như ở tuổi 49 mới hiểu thế nào là sự khác biệt của lão hoá nhân tạo và tự nhiên Doanh nhân Mailisa lên tiếng vụ sao kê của mẹ bé Bắp: Đó là để nói với con nít!
Doanh nhân Mailisa lên tiếng vụ sao kê của mẹ bé Bắp: Đó là để nói với con nít! Phẫu thuật không gây mê, bác sĩ khiến người phụ nữ tử vong
Phẫu thuật không gây mê, bác sĩ khiến người phụ nữ tử vong Mẹ bé Bắp hé lộ những tin nhắn chưa từng công bố về chuyến bay thương gia giữa lùm xùm từ thiện!
Mẹ bé Bắp hé lộ những tin nhắn chưa từng công bố về chuyến bay thương gia giữa lùm xùm từ thiện! Hot nhất hôm nay: Bạn gái Huỳnh Hiểu Minh sinh con gái, Angelababy lo sốt vó vì quyền thừa kế của quý tử thay đổi?
Hot nhất hôm nay: Bạn gái Huỳnh Hiểu Minh sinh con gái, Angelababy lo sốt vó vì quyền thừa kế của quý tử thay đổi? Sao nam "mất tích" khỏi Vbiz: Nghi chia tay đàn chị hơn 14 tuổi và gây xôn xao vì 1 tờ giấy nợ
Sao nam "mất tích" khỏi Vbiz: Nghi chia tay đàn chị hơn 14 tuổi và gây xôn xao vì 1 tờ giấy nợ Mẹ Bắp nói gì về thông tin "chuyển 2 tỷ đồng về quê cho ông bà ngoại trả nợ"?
Mẹ Bắp nói gì về thông tin "chuyển 2 tỷ đồng về quê cho ông bà ngoại trả nợ"? Vụ thi thể người phụ nữ cháy đen trong lô cao su ở Đồng Nai: Nghi do tự tử
Vụ thi thể người phụ nữ cháy đen trong lô cao su ở Đồng Nai: Nghi do tự tử Phạm Thoại chính thức tung ra 28 trang sao kê cho dân mạng check VAR
Phạm Thoại chính thức tung ra 28 trang sao kê cho dân mạng check VAR